Prognose Analyse (Predictive Analytics)
Predictive Analytics wird verwendet, um nicht bekannte Daten aus bekannten Daten zu ermitteln. Dies können z.B. zeitbasierte Verfahren sein, die zukünftige oder unbekannte Werte (abhängige Variablen) aus bekannten Werten (unabhängige Variablen) der Vergangenheit extrapolieren oder fehlende Datenelemente durch einen Abgleich mit vollständigen Datensätzen vorhersagen.
Eine prädiktive Analyse ist in den meisten Fällen nicht vollständig korrekt, da sie mit Annahmen und nicht vorhandenen Daten arbeitet, kann aber häufig die Datenqualität verbessern oder zumindest den subjektiven Informationsgehalt erhöhen.
Die vorhergesagten und die vorhandenen Datenattribute können entweder kontinuierlich (reelwertig) oder diskret sein. Ist der zu vorhersagende Wert diskret, so spricht man auch von einer Klassifikation – ein Sonderfall ist hier der binäre Fall, in dem nur zwei Möglichkeiten zur Vorhersage gegeben sind (positiv – negativ). Regressionsverfahren versuchen dagegen, die Parameter einer mathematischen Funktion so an eine Datenmenge anzugleichen, dass sie eine möglichst genaue Abbildung der gegebenen unabhängigen Variablen auf die abhängigen Variablen liefert. Diese wird meist dann eingesetzt, wenn sowohl die bekannten als auch die unbekannten Daten kontinuierlich sind.
ANKHOR bietet unterschiedliche Operatoren für Klassifikation und Regression:
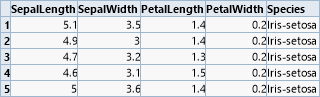
Vier der wichtigsten Klassifikationsoperatoren sollen nun an einem akademischen Beispiel gezeigt werden. Es handelt sich um den klassischen Datensatz zur Klassifikation von Schwertlilien ( Iris flower-Datensatz) von Sir Ronald Fisher. Hierbei werden vier kontinuierliche Attribute der Blütengröße genutzt, um zwischen drei Unterarten zu unterscheiden.
Der erste Schritt bei einer Analyse ist immer, sich einen Überblick über die Struktur der Daten und möglichen Zusammenhängen zu schaffen. Dies wird durch den Operator „dcanalyzewizard“ –Assistenten ermöglicht. Er liefert im oberen Bereich eine Zusammenfassung der Daten jeder Spalte, und im unteren Bereich die Korrelationen zwischen den Spalten.
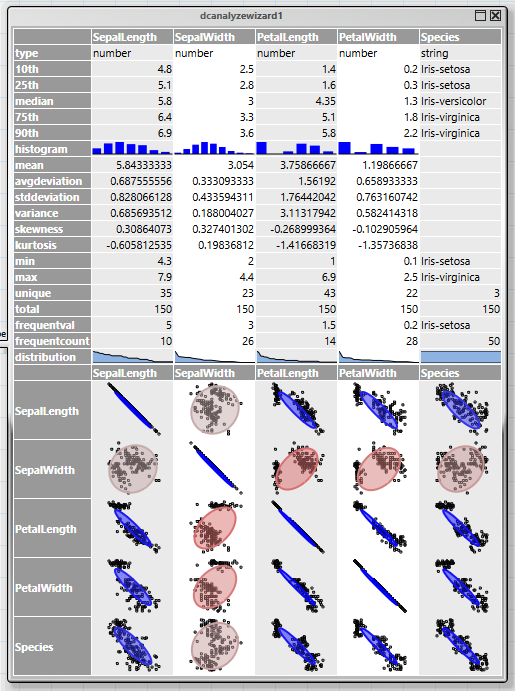
Die Korrelationsanzeige kombiniert zwei Diagrammformen, einen Scatterplot und eine Ellipse. Die Ellipse ist umso flacher, je stärker die Korrelation zweier Werte ist. Nicht korrelierte Spalten erscheinen als Kreise, vollständige Korrelation als Diagonale. In diesem Beispiel ist erkennbar, dass alle Blütengrößen mit der Ausnahme der „SepalWidth“ stark mit der Species korrelieren.
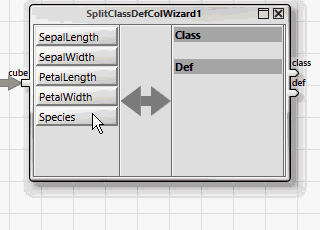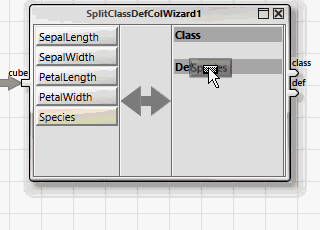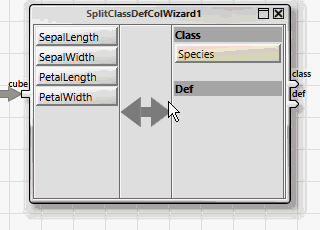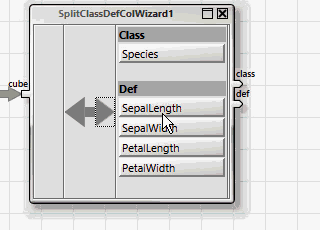
Alle ANKHOR-Operatoren für Klassifikation erwarten die abhängigen und unabhängigen Variablen in zwei getrennten Tabellen, „class“ für die abhängige Variable und „def“ für die unabhängigen. Dies kann einfach mit Hilfe des „SplitClassDefColWizard“-Assistenten erreicht werden.
Das einfachste lernende Verfahren zur Klassifikation nutzt einen Entscheidungsbaum. Dieser wird durch den „dtreebuild“-Operator erzeugt.
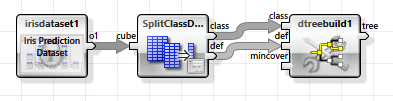
Der Entscheidungsbaum wird von links nach rechts abgearbeitet. An den inneren Knoten wird jeweils anhand eines unabhängigen Attributes eine der Abzweigungen genommen, die schließlich an den Blattknoten zu einer Entscheidung über das abhängige Attribut führen.
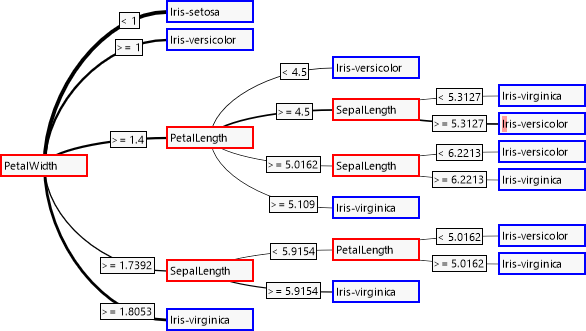
Wie schon anhand der Korrelationen zu erwarten war, wird das Attribut „SepalWidth“ nicht zur Entscheidungsfindung herangezogen. Die Dicke der Verbindungen zeigt, wie häufig eine Verbindung genommen wird. Der kleine rote Balken im vierten Blatt deutet darauf hin, dass dort eine fehlerhafte Klassifizierung vorgenommen wurde.
Eine genauere Analyse des Entscheidungsbaums kann mit Hilfe des „paiVisAnalyse“-Operators durchgeführt werden. Hierbei lassen wir alle abhängigen Werte des Datensatzes aus den unabhängigen mit Hilfe des Entscheidungsbaums bestimmen und vergleichen diese mit den tatsächlichen Werten.

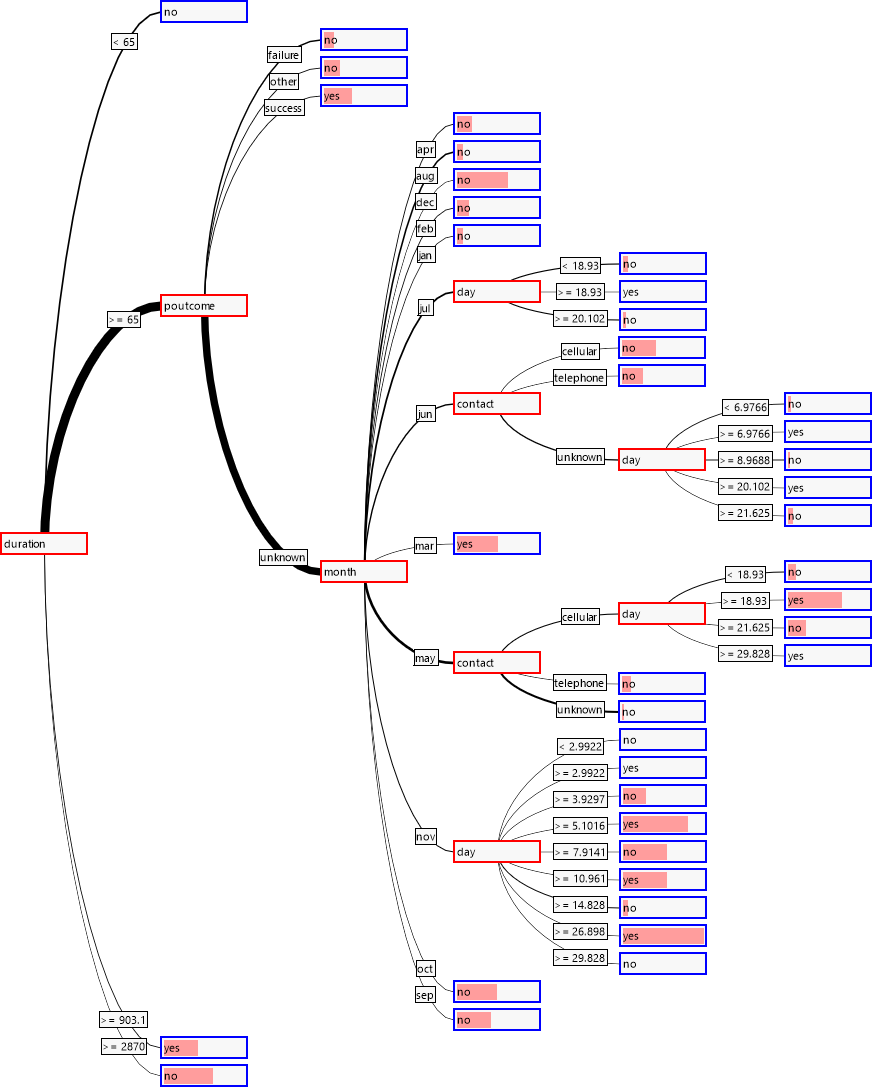
Das Resultat zeigt verschiedene Informationen:
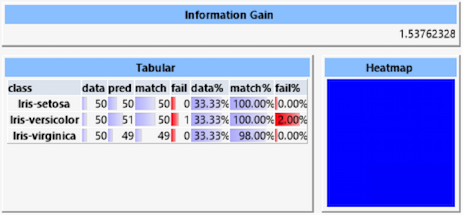
Der „Information Gain“ ist ein Maß für die durch die Vorhersage gewonnene Information. Dieser Wert ist umso höher, je genauer die Vorhersagegüte ist. Hierbei geht auch eine eventuelle Ungleichverteilung der Klassen im Datensatz ein. Die „Heatmap“ stellt die Abweichungen der vorhergesagten zu den tatsächlichen Klassen dar. Da die Vorhersage hier aber fast perfekt ist, ist die Anzeige gleichmäßig blau. In der Tabelle werden Werte für jede der Klassen aufgelistet:
- data: Anzahl der Datensätze mit dieser Klasse
- pred: Anzahl der Datensätze, für die diese Klasse vorhergesagt wurde
- match: Anzahl der korrekt vorhergesagten Datensätze
- fail: Anzahl der fälschlich dieser Klasse zugeordneten Datensätze
- data%: Prozentualer Anteil dieser Klasse am Datensatz
- match%: Prozentualer Anteil der korrekt vorhergesagten Datensätze
- fail%: Prozentualer Anteil fälschlich dieser Klasse zugeordneter Datensätze
Ein verwandter Algorithmus zur Klassifikation basiert auf dem Lernen logischer Regeln („rule finding“). Diese Regeln haben die Form von „und“-Kombinationen einfacher Relationen. Der „mrulelearn“-Operator liefert eine Liste von Regeln, die von oben nach unten abgearbeitet werden können. Jede Regel ist mit einer Klasse verbunden, und die erste Regel, die als wahr ausgewertet wird, bestimmt die entsprechende Klasse.
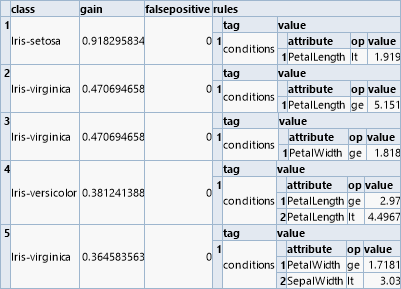
Im Gegensatz zum Entscheidungsbaum können die Regeln aber auch unabhängig betrachtet werden, um ihren Beitrag zur Vorhersage zu ermitteln.
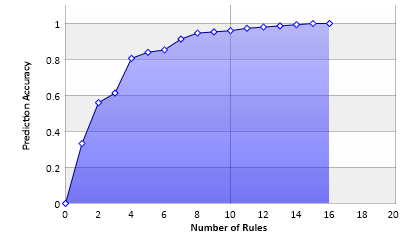
Dieses Diagramm zeigt die Genauigkeit der Vorhersage basierend auf der Zahl der verwendeten Regeln. Mit 16 Regeln kann eine hundertprozentige Vorhersage getroffen werden, allerdings decken die letzten drei Regeln jeweils nur noch jeweils einen einzelnen Fall ab.
Ein weiterer sehr einfacher Klassifizierungsalgorithmus basiert auf bedingten Wahrscheinlichkeiten. Der „Naive-Bayes“-Ansatz geht davon aus, dass alle unabhängigen Variablen auch unabhängig voneinander sind, sich also gegenseitig bei der Wahrscheinlichkeit für eine Klassenauswahl nicht beeinflussen.

Das Ergebnis der Vorhersage ist in diesem Beispiel nur leicht schlechter als beim Entscheidungsbaum, der Algorithmus selbst ist aber wesentlich einfacher und auch für große Datensätze mit sehr vielen unabhängigen Variablen geeignet.
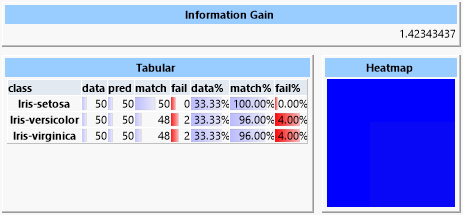
Zwei verwandte Algorithmen, die auf linearer Separierbarkeit basieren, sind lineare Diskriminanten-Analyse und logistische Regression. Die Klassen werden hier anhand von Hyperebenen unterschieden, die durch den N-dimensionalen Merkmalsraum der unabhängigen Variablen gelegt werden.
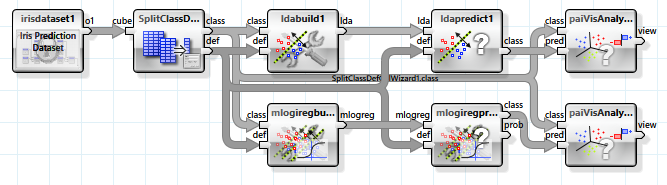
Da die Daten aber nicht vollständig linear separierbar sind, liefern diese Verfahren ein deutlich schlechteres Ergebnis. Besonders die lineare Diskriminanten-Analyse ist für die Problemstellung nicht geeignet.
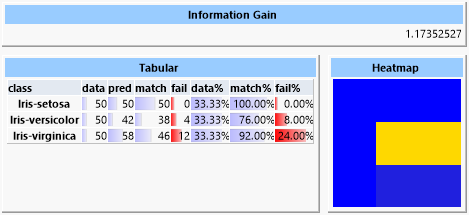
Man erkennt in der Heatmap die häufige Fehlklassifizierung zwischen Elementen der „versicolor“- und der „virginica“-Klasse. Die Heatmap stellt korrekte Vorhersagen blau, falsche Vorhersagen rot dar. Dazwischen liegen grün, gelb und orange. In der Zeile der Heatmap wird die tatsächliche Klasse, in der Spalte die vorhergesagte Klasse abgebildet. Es ist also ersichtlich, dass die „setosa“- und „verginica“-Klassen korrekt zugeordnet werden konnten, aber die Elemente der „versicolor“-Klasse häufig falsch als „virginica“ eingeordnet wurden.
Ein wesentlich mächtigerer Ansatz, der auch auf der linearen Separierbarkeit basiert, ist die „Support-Vector-Maschine“. Allerdings werden hierbei die unabhängigen Variablen mit Hilfe einer nicht linearen Abbildung in einen höherdimensionalen Raum abgebildet, in dem sich mehr Möglichkeiten zur Separierbarkeit ergeben. In diesem Beispiel wird eine Abbildung mit einem polynomiellen Kernel genutzt. Da die Anzahl der Dimensionen sehr groß (bis unendlich) sein kann, wird diese nicht tatsächlich durchgeführt, stattdessen wird ein Trick genutzt, mit dem das Ergebnis eines Skalarprodukts zweier Merkmalsvektoren im Abbildungsraum direkt berechnet werden kann. Somit werden auch nicht die Parameter der trennenden Hyperebene, sondern Stützvektoren aus der Menge der Merkmalsvektoren gespeichert.
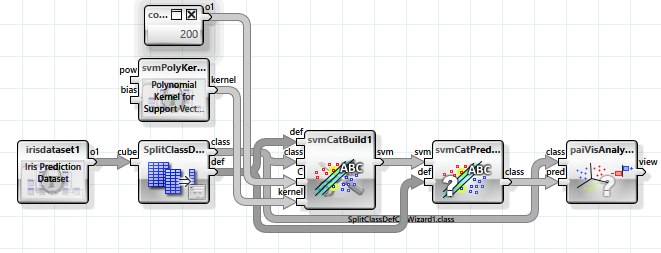
Mehrere Parameter können zur Konfiguration des Klassifikators verwendet werden.
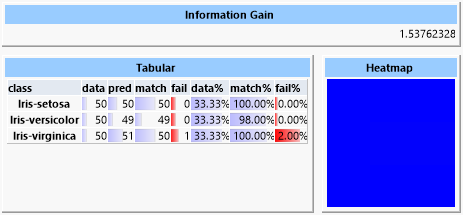
Eine Support-Vector-Maschine ist sehr effektiv in der Bestimmung der Klassen, benötigt aber sehr viel Trainingszeit, die mehr als überproportional mit der Anzahl der Trainingsdaten ansteigt.
Als letzter Algorithmus sollen noch die selbstorganisierenden Karten erwähnt werden. Diese lernen in einem ersten Schritt unüberwacht (also ohne die abhängige Variable zu kennen) ein Abbildungsverfahren aus dem mehrdimensionalen Merkmalsraum in einen zweidimensionalen Raum. In einem zweiten Schritt wird dann dieser reduzierte Merkmalsraum entsprechend der Klasse der dort vorherrschenden Datenelemente eingefärbt, so dass eine Vorhersage dann durch eine Abbildung und ein direktes Nachsehen in dieser Karte erreicht werden kann.
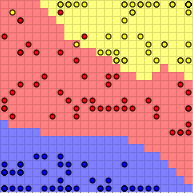
Ein komplizierteres Beispiel mit Echtweltdaten basiert auf den Ergebnissen einer Telemarketing-Kampagne einer Bank (Quelle: http://archive.ics.uci.edu/ml/datasets/Bank+Marketing). Die Tabelle enthält mehrere Parameter, die Kunden der Bank betreffen, und die Information, ob ein Anruf bei dem Kunden zu einem Verkauf eines Produkts führte. Das Ziel der Prediction ist, einen Klassifikator zu erzeugen, anhand dessen die Gruppe der Kunden so eingeschränkt werden kann, dass die Wahrscheinlichkeit eines Verkaufs erhöht und somit die Marketingmaßname effektiver eingesetzt werden kann.
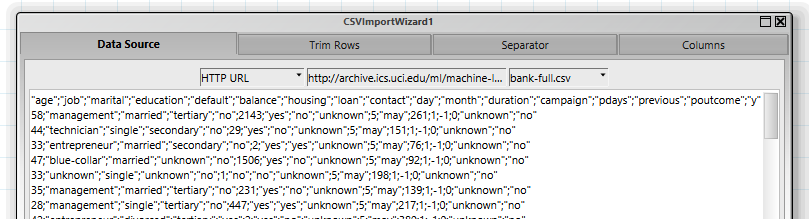
Der erste Schritt ist, die Daten, die als csv-Datei in einem Zip-Archiv vorliegen, einzulesen. Dies wird am einfachsten mit dem „CSVImportWizard“-Assistenten erlegt, der sowohl den Download der Daten als auch die Konvertierung in eine Tabelle durchführt.
Ein erster Blick auf die Korrelationen zwischen den einzelnen unabhängigen Variablen und der abhängigen Variablen zeigt, dass drei der Variablen mit hoher Wahrscheinlichkeit als besonders relevant für die Klassifikation eingestuft werden können: „duration“, „poutcome“ und „month“.

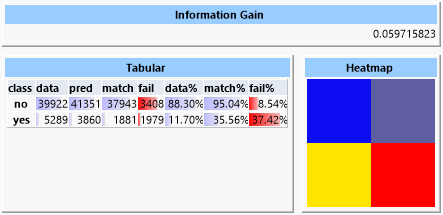
Ein erster Versuch mit einem “Naïve Bayes Predictor“ zeigt einen Informationsgewinn von ca. 0.06.
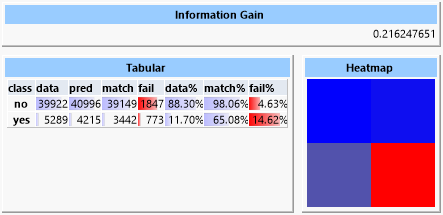
Ein Entscheidungsbaum dagegen bringt einen Informationsgewinn von ca. 0.22.
Der Grund dafür findet sich bei einer genaueren Inspektion des Baumes, er enthält fast 6000 Blätter, hat sich also sehr genau an die Daten angenähert. Es ist zu bezweifeln, dass dieser Baum den gleichen Erfolg bei anderen Daten haben würde.

Um bewerten zu können, wie gut die Vorhersage nicht für die exakt gleichen, sondern ähnliche Daten ausfallen würde, teilen wir den Datensatz in zwei Hälfen, einen Trainings- und einen Evaluierungsdatensatz, und verwenden diese Hälften entsprechend.
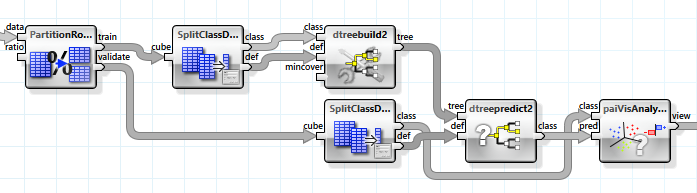
Der Informationsgewinn beträgt nun nur noch 0.05, der Baum hat aber immer noch ca. 4500 Blätter. Um einen allgemeineren Baum zu erhalten, setzen wir den „mincover“-Wert, also den Anteil der Datensätze, die jedes Blatt abdecken muss, auf 4% (dieser Wert wurde experimentell ermittelt). Der Baum hat nun nur noch 39 Blätter, erreicht aber einen Informationsgewinn von 0.079.
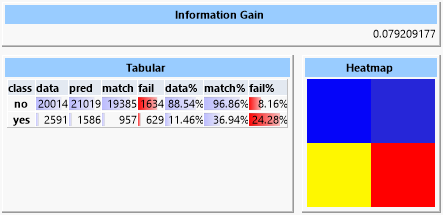
Betrachten wir den Baum, sehen wir auch, dass die erwarteten Variablen nahe bei der Wurzel liegen.
Zum Vergleich betrachten wir nun noch eine Vorhersage mit Regelsuche.
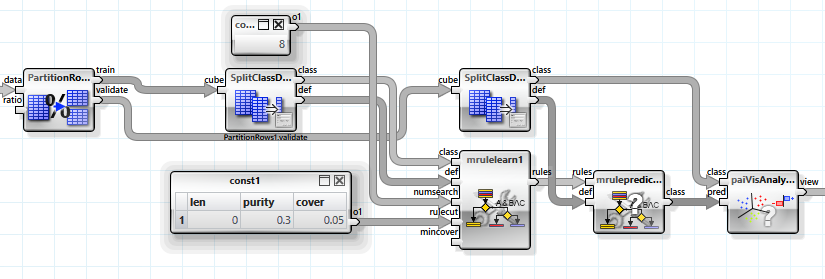
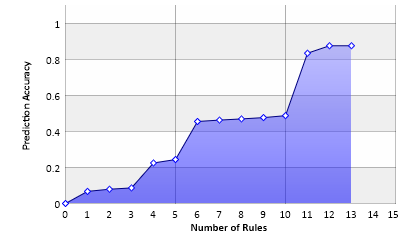
Die Werte für „purity“ und „cover“ wurden experimentell bestimmt. Es ergibt sich ein Informationsgewinn von ca. 0.11, wobei 13 Regeln gefunden wurden.
Man erkennt, dass ein paar wenige Regeln die Vorhersage dominieren.
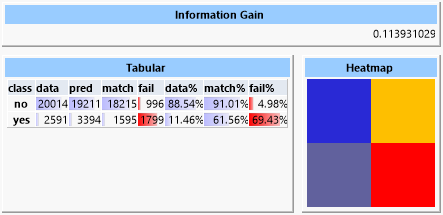
Auch wenn der Informationsgewinn bei diesem Beispiel nur recht gering ist, so ist doch sowohl beim „yes“-als auch beim „no“-Fall die Rate der erkannten Datensätze deutlich höher, als durch eine reine Zufallsverteilung anzunehmen wäre (61.56% gegen 11.46% beim positiven Fall). Somit wird das Ziel erreicht, die Gruppe der Kunden kann bei erhöhter Erfolgswahrscheinlichkeit eingeschränkt werden.
Der geringe Informationsgewinn ist natürlich auch darin begründet, dass im Datensatz durch die ungleiche Dichte der beiden Klassen auch nur ein geringer Informationsgehalt vorhanden ist.
Klassifikatoren in ANKHOR:
| Verfahren | Typen | Vor-/Nachteile |
|---|---|---|
|
Entscheidungsbaum |
Beliebig |
|
|
Regelsuche |
Beliebig |
|
|
Naive Bayes |
Beliebig |
|
|
Zufallswald |
Beliebig |
|
|
Nächster Nachbar |
Kontinuierlich |
|
|
Support-Vector-Maschine |
Kontinuierlich |
|
|
Neuronales Netz |
Kontinuierlich |
|
|
Lineare Diskriminanten |
Kontinuierlich |
|
|
Logistische Regression |
Kontinuierlich |
|
|
Selbstorganisierende Karten |
Kontinuierlich |
|